[Algorithm] Sorting

Big O란? 알고리즘의 퍼포먼스를 이해하기 쉽고 효율적으로 작성하는 방식

 

Sorting은 A-Z까지 정렬하거나 큰수에서 작은수, 이진 검색처럼 빠른 알고리즘을 사용하려면 일단 먼저 배열 정렬을 해야한다.

 

1. 버블정렬

장점 : 쉬움

단점 : 자주 사용되지는 않음

두개의 아이템을 비교하고 오른쪽으로 반복해서 이동하는 방법으로 비교하고 스와핑의 반복이다.

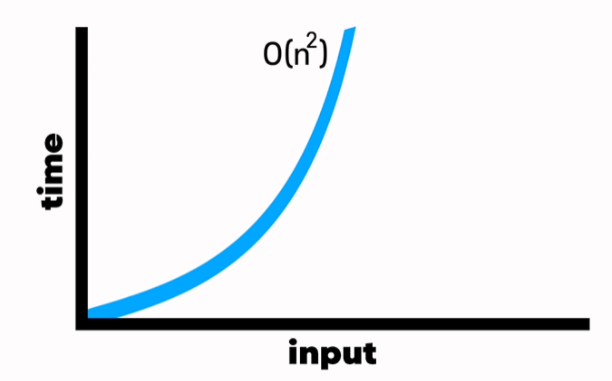
Big O ⇒

최악의 경우 모든 수를 다 스왑해야한다. 따라서 모든 사이클 마다 아이템을 교환해야해서 O(n^2)이다.

 

 

2. 선택정렬

전체 아이템중에서 가장 작은 아이템의 위치를 정하고 그 위치를 변수에 저장한다.

앞에서 부터 비교해 나가면서 지정해둔 가장 작은 숫자보다 크면 가장 작은 아이템의 위치의 수와 스왑한다.

그리고 처음 스왑해서 위치가 저장된 수를 제외하고, 다음사이클은 스왑하지 않은 수중(정렬되지 않는 수 중) 에서 가장 작은 값을 선택한다. 그리고 두번째 수와 비교하고 스왑한다.

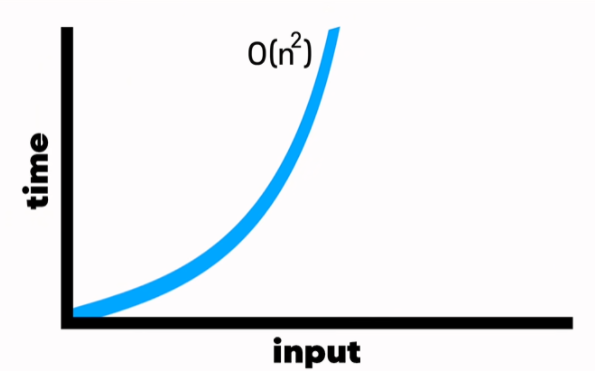
선택정렬은 버블정렬과 유사하고 스왑도 있고 비교도 있다. 정렬 되지 않은 배열에서 작은 수를 찾으므로 n-1이다. 따라서 시간 복잡도는 O(n^2)로 버블 정렬괴 동일하다. 하지만 한번의 스압만이 필요하기 때문에 최악의 경우가 버블정렬보다 낫다.

3. 삽입정렬

인덱스 1부터 시작하는데 왼쪽과 비교해서 작을경우 스왑, 크면 그대로 둔다 그리고 인덱스 2와 왼쪽을 비교해서 작으면 스왑, 크면 그대로 둔다. 그리고 인덱스 0과 인덱스 1을 비교해서 작으면 스왑, 크면 그대로 둔다.

이는 삽입정렬 모든 아이템을 스캔해야하지만 삽입정렬은 필요한 아이템만 스캔하기때문 선택정렬보다 빠르다.

하지만 시간 복잡도는 동일하게 O(n^2)이다.

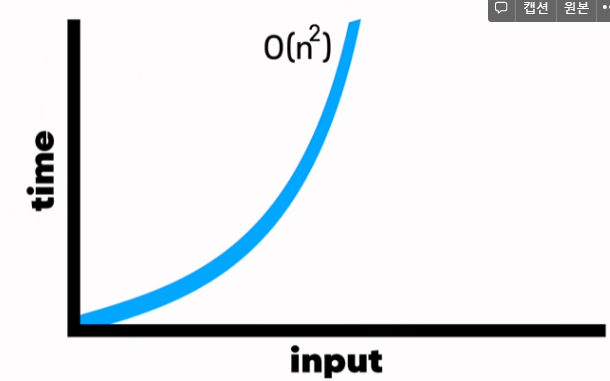
이처럼 세개의 알고리즘은 각기 매우 다르지만 왜 Big O(시간복잡도)는 동일할까?

이러한 경우는 최악의 시나리오는 보지말고 평균 시나리오를 봐야한다.

최악과 최고의 케이스는 자주 발생하지 않고 대부분 평균에 해당하기 때문에 그것을 감안하고 알고리즘을 봐야한다.